Музыка — это бессознательное упражнение души в арифметике.
Арифметика музыки | Юный техник 1981-06

Г. Лейбниц
А что, если уделить полчаса упражнению сознательному? Ну хотя бы попытаться выяснить, как человек выбрал те семь нот, из которых построил всё грандиозное здание музыки.
Вопросы возникают уже при взгляде на клавиатуру фортепиано, часть которой изображена для наглядности на рисунке. Почему одни клавиши белые, другие чёрные? Почему чёрные располагаются не симметрично, а группами по две и по три? Почему между двумя соседними белыми клавишами кое-где нет чёрной? Почему белые клавиши имеют собственные названия, а чёрные не имеют? Почему, наконец, с каждой восьмой белой клавиши отсчёт названий повторяется?
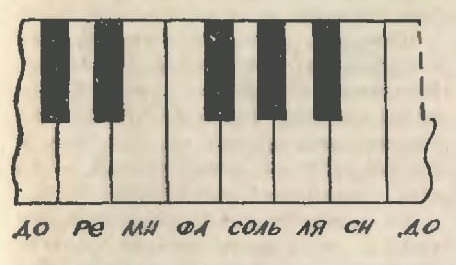
Ответы на все эти вопросы даёт арифметика. Правда, придётся слегка вспомнить и физику. А чтобы ответы были полнее, затронем и историю строительного материала музыки. Во имя ясности и краткости нам придётся что-то предельно упрощать, а что-то смещать во времени, но эти вольности не будут касаться сути.
Из школьного курса физики вы знаете, что звук — это колебания какого-нибудь тела, передаваемые окружающему воздуху, а от него нашему уху. Музыкальный звук отличается от любого другого прежде всего постоянной и определённой частотой колебаний. Самый низкий музыкальный звук — это 18 колебаний в секунду, или 18 герц. Более низкие частоты ухо уже не воспринимает. Самый высокий — 4700 герц. Звуки выше этого предела хоть ухо и слышит, но они кажутся скорее писком, чем музыкальным звуком. Количество колебаний определяет основную характеристику музыкального звука — его высоту. Она-то нам и понадобится, а остальных трёх характеристик — силы, тембра и длительности — мы коснёмся мимоходом.
Наше ухо очень чувствительно, в пределах музыкального диапазона, границы которого мы обозначили, оно замечает изменение частоты всего на один герц. Естественно предположить, что музыкальных звуков должно быть почти 4700. Но их не набирается и сотни. 88 клавиш фортепиано — это почти всё, что мы имеем. Ниже могут опуститься только несколько самых больших труб органа, а выше забирается лишь миниатюрная флейта-пикколо. Человек выбрал меньше ста разных частот из нескольких тысяч возможных, а остальные оставил вне музыки вообще.
На чём же основывался выбор? Есть ли тут система?
Конечно, есть. Часть этой системы — деление музыкального диапазона на октавы. Чтобы было понятнее, что это такое, сделаем небольшое сравнение.
Положите перед собой метровую линейку или хотя бы представьте себе ее. Метр делится на дециметры. 10, 20, 30, 40 сантиметров и так далее. Если брать каждый дециметр отдельно, он будет равен любому другому.
Октавы тоже равны между собой, но числовая последовательность здесь сложнее. Если вы возьмете в левой части клавиатуры звук «ля» с частотой 55 герц, а потом будете поочередно нажимать каждую восьмую вправо белую клавишу, вы получите такой ряд частот: 55, 110, 220, 440, 880, 1760, 3520. Частоты не прибавляются, как дециметры, а удваиваются.
И то и другое легко объясняется. Счет десятками произошел от десяти пальцев на руках. Каждое круглое число завершало предыдущий десяток и служило точкой отсчета для нового. А здесь каждый восьмой звук завершает одну октаву и открывает следующую, отсюда и значение слова «октава» — восьмой. Как пальцы определили границы десятков, так наш слух определил границы октав. Звук с частотой вдвое больше кажется нам хоть и выше предыдущего, но очень похожим на него по восприятию Ухо, сравнивая эти два звука, наделяет их одним качеством. Причем они настолько близки по характеру, что если взять их одновременно, мы услышим не два звука, а один. Никакое другое соотношение частот не дает такого эффекта. Естественно, не имело смысла считать разными столь похожие звуки. Вот почему с каждой восьмой клавиши, то есть с каждого удвоения частоты, начинается тот же отсчет названий. А чтобы отличать одну октаву от другой, им тоже дали названия. Посередине клавиатуры размещается наиболее употребительная первая октава. Вправо от нее — вторая, третья, четвертая и кусочек пятой. Влево — малая октава, большая, контроктава и кусочек субконтроктавы.
Частоты звуков внутри октавы тоже не подчиняются такой простой последовательности, как сантиметры в дециметрах. Скажем, звук «ля» первой октавы — 440 герц. Но если мы нажмём соседнюю справа белую клавишу, получим сразу 494 герца. Еще одну соседнюю — 523 герца. Вроде бы никаких закономерностей не наблюдается. Но они есть и здесь. Количество звуков внутри октавы и их относительную высоту подсказала природа. Оказывается, уже тетива лука, колеблясь после выстрела, давала весь набор музыкальных звуков, которыми мы почти без изменений пользуемся до сих пор. Еще не было музыкальных инструментов, не было и самой музыки, а материал для нее уже был!
С точки зрения физики тетива и струна — одно и то же. Да и сделал человек струну, обратив внимание на свойства тетивы. А звучащая струна, как и тетива, колеблется не только целиком, но одновременно и частями — половинками, третями, четвертями и так далее. Половинки колеблются вдвое чаще, чем целая струна, трети — втрое, четверти — вчетверо. Словом, во сколько раз меньше колеблющаяся часть струны, во столько же раз больше частота ее колебаний. Следовательно, струна одновременно издает и основной тон, и еще какое-то количество разных призвуков.
Попробуем определить, каких именно.
Допустим, вся длина струны колеблется с частотой 24 герца. Это число выбрано произвольно, чтобы удобнее было считать. При любой другой исходной частоте соотношения получатся одинаковыми, потом вы сможете, если захотите, проверить это. И вообще в музыке важны прежде всего соотношения звуков, а не их абсолютная высота. Это легко доказывается: некоторые песни вы наверняка слышали в исполнении и баса и тенора, при этом менялись абсолютные частоты звуков, могло измениться и ваше впечатление от разных голосов, но ни на йоту не исказилась мелодия, потому что соотношения ее звуков по высоте остались одинаковыми. Кстати, эталонная частота звука «ля» первой октавы, от которого идет настройка инструмента, несколько раз менялась, но это никак не мешало слушать музыку, написанную до изменения эталона.
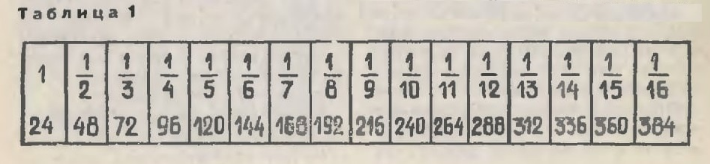
Итак, мы взяли струну, которая колеблется с частотой 24 герца. Вычисляя колебания долей, мы получим ряд чисел (табл. 1). Эта последовательность частот так и называется — натуральный, то есть природный, звукоряд.
Вы можете возразить: мол, ни тетиву, ни струну нельзя считать природными телами, потому что их сделал человек. Возьмем тогда безусловно природное тело — полый ствол какого-нибудь растения. Оказывается, мы не можем заставить столб воздуха в стволе колебаться неравными частями. Только целиком, или половинками, или третями и так далее. И если целый столб воздуха колеблется с частотой 24 герца, то половинки дадут 48 герц, трети — 72 и так далее. Если мы возьмем Другую исходную частоту, все равно соотношения выстроятся точно так же.
До сих пор среди музыкальных инструментов сохранились трубы, которые не имеют ни клапанов, ни вентилей, ни боковых отверстий. Например, фанфара. Играют на ней, следуя только законам природы: по-разному напрягая губы и кончик языка, заставляют столб воздуха колебаться различными долями. И если основной тон фанфары мы примем за 24 герца, музыкант никак не сможет выжать из нее звук с частотой между 24 и 48 герцами. Потом пойдет 72, 96 и так далее.
Следовательно, природный звукоряд совершенно одинаков и для тетивы, и для струны, и для пустотелого ствола дерева, и для фанфары.
Но вернёмся к струне. Возникает попутный вопрос: если столб воздуха в трубе может издавать различные частоты поочередно, то струна-то издает их все сразу! Почему же мы слышим только основной тон?
Тут вступает в действие вторая характеристика музыкального звука — его сила. Амплитуда колебаний целой струны значительно больше, чем ее частей, поэтому призвуки слышны гораздо слабее основного тона. А в совокупности они, накладываясь друг на друга, составляют тембр — третью характеристику музыкального звука. Инструмент, по-разному резонируя тем или иным частотам, может влиять на тембр: гитара, например, лучше подчеркивает низкие частоты, а домра — высокие.
Мы уже выяснили, что частоты, отличающиеся друг от друга вдвое, составляют границы октавы. В полученном нами ряду между частотами 24 и 48 пока никаких других частот нет. Между 48 и 96 появилась частота 72. Между 96 и 192 — три частоты. А между 192 и 384 — уже полная природная октава, то есть тот материал, который не нужно было и выбирать — он дан готовым.
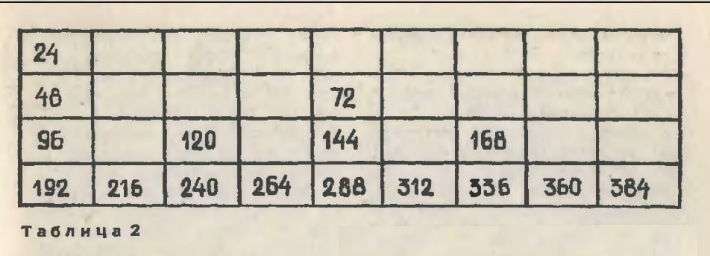
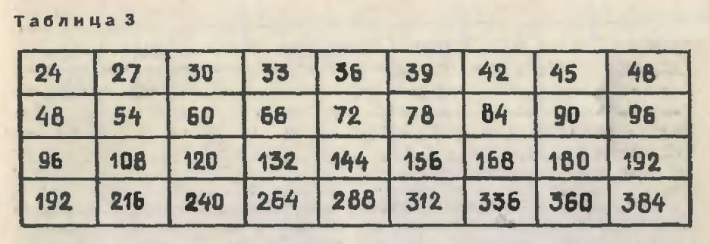
Для наглядности расположим наш материал так, как это сделано в таблице 2. Здесь частоты, отличающиеся друг от друга вдвое, расположены по вертикали, и только границы полной октавы лежат в одном ряду. Опираясь на то, что нам уже известно, мы можем заполнить пустые клетки этой таблицы, то есть восполнить недостающие в других октавах звуки. В каждую пустую клетку впишем делённую на два частоту из клетки, расположенной ниже. У нас возникнет картина, изображенная в таблице 3. Мы получили четыре полные натуральные октавы.
Но вот еще один вопрос, с виду вроде бы малосущественный, но по сути очень важный. Почему человек ограничил натуральный звукоряд шестнадцатью призвуками? Ведь струна, если иметь в виду идеальное физическое тело, может колебаться бесконечно малыми долями, а значит, и число призвуков теоретически можно продолжать бесконечно.
На этот вопрос можно ответить очень просто. Например, так: реальная струна отличается от идеальной тем, что имеет толщину, плотность и предельную длину, поэтому ограничено и число призвуков. Или так: ни на одном духовом инструменте не удалось поделить колеблющийся в нем воздух больше чем на шестнадцать долей. Но действительный ответ выглядит серьезнее.
Дело в том, что существование натурального звукоряда стало известно человеку гораздо позже, чем оформился и получил распространение определенный строй музыкальных инструментов. Другими словами, если натуральный звукоряд был заложен в природе с самого начала, то есть задолго до появления музыки, то открыли его уже тогда, когда существовал развитый и в принципе не отличающийся от нынешнего музыкальный строй. Человек интуитивно подстраивал струны между собой так, чтобы они создавали благозвучие. Были инструменты и с одной струной — монохорды. Поначалу его гриф делался гладким, без порожков, и музыкант просто скользил пальцем по струне как угодно. Но потом он интуитивно нащупал точки, где звуки получались наиболее естественными, и оснастил эти места грифа порожками. И вот, когда люди открыли природный звукоряд, изучили его и сравнили с тем, что бытовал у музыкантов, оказалось, что первые шестнадцать призвуков природного звукоряда почти точно совпадают со строем музыкального инструмента. Слух опередил научные исследования, и получается, что человек, занимаясь музыкой, и в самом деле бессознательно упражнялся в арифметике!
Но мы отметили; что совпадение оказалось почти точным. В чем же заключалось это «почти»?
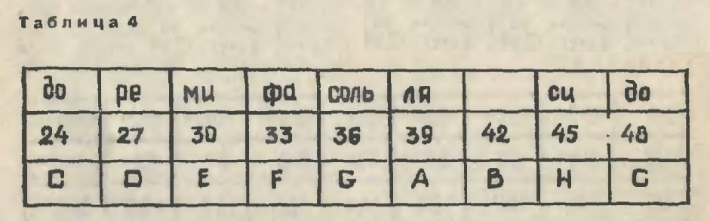
Взгляните на таблицу 4 — мы выделили в ней одну октаву, верхнюю из предыдущей таблицы, проставив знакомые нам нотные названия звуков и буквенные обозначения ступеней натуральной октавы. Вы сразу обратили внимание, что в нашей привычной нотной системе нет одной частоты из природного звукоряда. Это первое расхождение. И второе: в натуральном звукоряде есть частоты 33 и 39, есть они и в таблице 4, но в следующей вместо них появятся частоты 32 и 40. Вот и вся разница. Но чем же она вызвана?
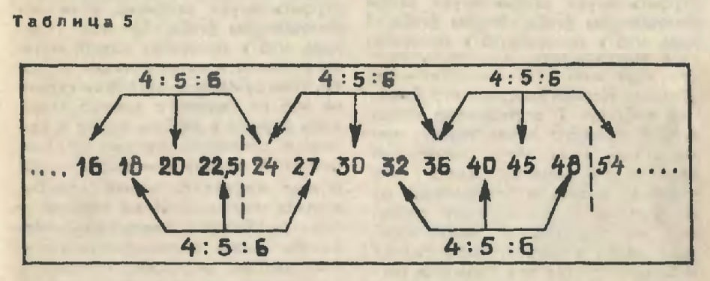
Ухо человека оказалось более взыскательным, чем природа, предложившая натуральный звукоряд. Музыканты обратили внимание, что сочетание некоторых трех звуков между собой особенно естественно. Потом выяснилось, что это были частоты, относящиеся друг к другу как 4:5:6. В каждой природной октаве есть только одно такое сочетание — в нашем примере это 24 : 30 : 36. А музыканты настраивали свои инструменты так, что весь звукоряд превратился в сплошную цепь приятных для слуха, то есть гармонических, трезвучий с соотношением частот 4:5:6. Чтобы убедиться в этом, продолжим немного нашу октаву вправо и влево. Как это делается, вы уже знаете: вправо соответствующие частоты умножаются на два, влево — делятся на два (табл. 5). Видите, как изменился звукоряд от небольших поправок!
Этот ряд, родившийся еще в Древней Греции, в разных странах называется хоть и по-разному, но удивительно схоже: в переводе на русский язык получается «согласие», «порядок», «стройность» и даже «мир». А в самом русском языке такая упорядоченная последовательность звуков называется прекрасным словом «лад».

В музыке у слова «лад» есть и другое значение. Посмотрите на таблицу 6. В ней указано отношение каждой последующей частоты к предыдущей. Эти отношения неодинаковы. Если считать девять восьмых и десять девятых целым тоном, то шестнадцать пятнадцатых составляют примерно половину целого тона. Значит, к ладу можно присмотреться и с другой стороны — как к чередованию целых тонов и полутонов. И вот что открыли древние музыканты: от этого чередования зависит характер музыки. Скажем, если взять за основу мелодии звук «до», то полутон будет третьим по счету и мелодия получится радостной. А если взять за основу звук «ля», полутон пойдёт вторым и мелодия получится грустной. Так появились мажорный и минорный лады. Частоты и их последовательность в звукоряде те же, но в разных мелодиях меняется последовательность тонов и полутонов.
До сих пор мы говорили только о семи звуках в октаве, представленных белыми клавишами. Теперь о чёрных.
Вообще-то ладу вполне хватало семи звуков и хватило бы до сих пор, но некоторые музыкальные инструменты вынудили ввести еще пять вспомогательных. Давайте посмотрим, как это было.
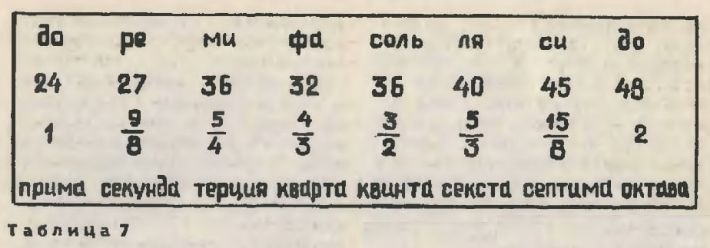
В таблице 7 определено отношение каждого звука лада к начальному, если этот начальный принять за единицу. Здесь же указаны названия интервалов по отношению к начальному звуку, они же определяют место каждого звука в октаве. Переводятся и запоминаются эти термины легко: «прима» — первый, «секунда» — второй, «терция» — третий и так далее. Лад — это прежде всего соотношения звуков, а не сами частоты. В других октавах частоты иные, но соотношения остаются теми же.
Теперь представьте, что вы выучили какую-то мажорную мелодию, которая начинается с «до», но вам вдруг понадобилось сыграть ее с «ре», то есть в другой тональности. Естественно, вам нужно сохранить соотношения. Попробуем же взять в качестве основного звука частоту 27 и выстроить звуки согласно этим соотношениям (табл. 8).
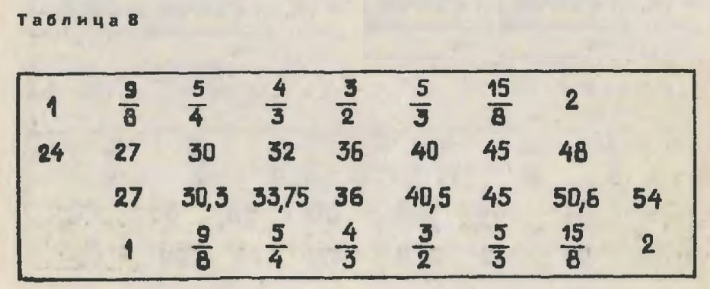
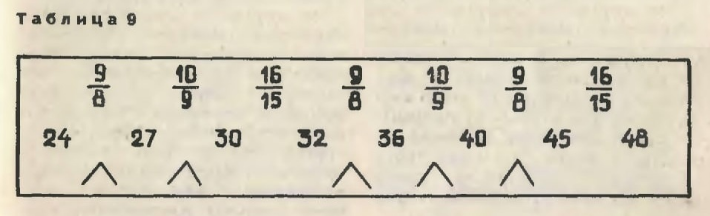
Мы увидим, что в пределах нашей октавы появились четыре новых частоты. Инструменту наподобие скрипки это не страшно: можно зажимать струны в любом месте и тем самым сохранить нужные соотношения. А органу или фортепиано? Нужно добавлять новые трубы, струны, клавиши. И не четыре, а гораздо больше: ведь мы хотели бы иметь возможность начинать любую мелодию, мажорную или минорную, с любого звука октавы. Подсчитано, что для этого нам нужно было бы иметь в каждой октаве не семь звуков, а восемьдесят пять. Играть на таком инструменте, конечно же, было бы невозможно. Древние греки нашли компромиссное решение. Они добавили новые звуки только там, где интервал между основными звуками равнялся целому тону. Не разделили целые тона пополам, нет, ведь это неделимые элементы лада, а просто ввели вспомогательные звуки. У них даже нет собственных названий, а именуются они, например, «до диез», что означает «выше до», или «ми бемоль», то есть «ниже ми». Причем один и тот же дополнительный звук можно назвать двояко. Если, скажем, он стоит между «до» и «ре», это и «до диез», и «ре бемоль». Вглядитесь в таблицу 9 — не напоминает ли вам расположение новых звуков чёрные клавиши фортепиано? Так оно и есть. Вот откуда происходит форма клавиатуры — ещё от древних греков.
(Заметим в скобках, что если в какой-то местности бытует один лад и используется одна тональность, то инструмент здесь по-прежнему может обходиться семью звуками в октаве, как, например, прекрасно обходятся до сих пор некоторые гармошки.)
Но, конечно, добавление пяти звуков пока не до конца решило проблему. Соотношения между соседними звуками все равно оставались разными, искусственно введенные полутона не были равны исконным полутонам лада, и не из любой тональности в любую можно было переходить легко и просто.
И тут мы обязаны вспомнить Пифагора. То, что он был учёным, знают все. А то, что он был еще и музыкантом, знают немногие. Сочетание этих дарований позволило Пифагору первым открыть существование натурального звукоряда. Пифагор проделал множество опытов с монохордом. Делил струну на части, прислушивался, наблюдал колебания. Эти опыты Пифагора легли в основу науки, которую мы называем сейчас музыкальной акустикой. Он же, следуя собственной теории совершенства малых чисел, объяснял основы гармонии так: наиболее естественно воспринимаются ухом частоты, которые находятся между собой в простых числовых соотношениях. Вот откуда и октава 1:2, и трезвучие 4:5:6.
Разобравшись в физике и математике музыки, Пифагор помог музыкантам решить и сугубо практическую задачу: как настроить инструмент, чтобы не увеличивать количество звуков в каждой октаве сверх двенадцати и в то же время дать возможность музыканту свободно переходить из тональности в тональность и из лада в лад.

Внутри октавы наиболее слитно с основным тоном воспринимается квинта, которая составляет с ним тоже простое соотношение 3 : 2. Пифагор решил поэтому взять квинту за основу строя и вывел удивительно красивую формулу (табл. 10). А если объяснить её словами, он решил сперва выстроить все двенадцать звуков по точным квинтам, а потом делением и умножением на два свести их в одну октаву. Почему Пифагор не поставил единицу слева и не выстроил вправо двенадцать последовательных квинт? Дело в том, что нужно было сохранить чистой и кварту, потому что это обратная квинта — в нашем примере 32 от 48.
Попробуем восстановить ход мысли Пифагора. За единицу возьмём частоту, к которой мы уже привыкли. Это 48 — граница нашей октавы. Теперь вправо отложим три вторых от этого числа, потом три вторых от получившегося и так далее. А влево — две трети от 48, потом две трети от получившегося и так далее (табл. 11, вверху). Крайние звуки одного качества: «фа диез» — это одно и то же, что «соль бемоль». Круг должен вроде бы замкнуться. Попытаемся его замкнуть. Последовательным умножением левого числа на два, то есть октавами, приходим к крайнему правому числу (табл. 11, снизу). Не сошлось! Двенадцать квинт не равны семи октавам. Это расхождение так и называется пифагоровой коммой.

Посмотрим, что же получилось в итоге. Сведем верхние числа таблицы 11 в нашу октаву, то есть последовательным делением правых чисел на два и умножением левых чисел на два уложим результаты в промежуток между частотами 24 и 48.
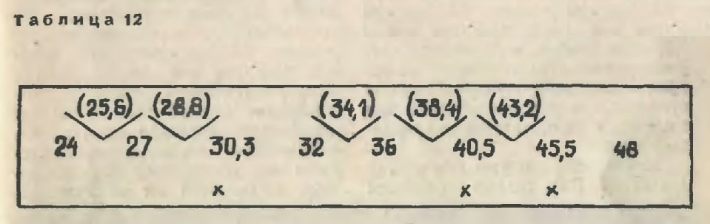
Мы увидим, что лад изменился весьма незначительно (табл. 12). Всего три частоты (они помечены крестиками) слегка отклонились от первоначальных, зато интервалы более или менее выровнялись. Музыканты, пользуясь теми же двенадцатью звуками, получили возможность переходить из тональности в тональность и из лада в лад гораздо свободнее. Поэтому пифагоров строй продержался больше двух тысяч лет.
Но никуда нельзя было деть пифагорову комму — она оставалась. Настройщики кое-как распределяли ее, сохраняя чистыми квинты и кварты, а музыкант должен был проявлять изворотливость, чтобы избежать фальшивых звуков, которые были прозваны «волками». Особенно досадовали органисты: ведь органу присуща уникальная длительность звука — четвертая и последняя его характеристика. Одно дело фальшь на клавесине, там звук быстро затухает, и совсем другое, когда волком воет орган!
Неудивительно поэтому, что очередную и пока последнюю реформу предложил в 1691 году именно органист — Андреас Веркмейстер. Он сформулировал задачу так. Первое: нужно сохранить в октаве двенадцать устоявшихся звуков. Второе: все соотношения между соседними частотами должны быть абсолютно равными. Поставленная таким образом задача имеет единственное решение: каждая последующая частота будет относиться к предыдущей так, как корень двенадцатой степени из двух относится к единице.
Правда, квинта при этом пострадала. Этот считавшийся незыблемым интервал стал короче. Как вы догадываетесь, ровно настолько, что теперь двенадцать квинт точно укладывались в семь октав. Но изменение было настолько незначительным, что только очень тонкий слух мог уловить «тупые» квинты. Изменились, но тоже слегка, и все другие интервалы. Чистой осталась только октава.
Достоинства нового строя постепенно стали очевидными почти всем. Исчезли «волки». Стало возможным переходить из тональности в тональность и из лада в лад как угодно. В самом ладу, естественно, остались те же семь основных звуков, но теперь любой лад мог открываться с любой клавиши, хоть с черной, и тогда некоторые белые клавиши становились дополнительными, а не основными. Так что сейчас клавиши двух цветов и двух размеров — лишь дань традиции, потому что все звуки уравнялись в правах.
Можно было бы привести еще одну таблицу, но лучше всего представить себе новую музыкальную шкалу, глянув на гриф гитары. Каждое расстояние между порожками относится к соседнему, меньшему, как корень двенадцатой степени из двух относится к единице.
Казалось бы, все хорошо, но проблемы остались. Например, строй оркестра Фортепиано, челеста, ксилофон, орган настраиваются по Веркмейстеру. Вся скрипичная группа может играть в чистом строе, но вынуждена подлаживаться. А фанфара и хотела бы подладиться, да не может. Ведь труба, гни её или скручивай, остается трубой, физическим телом, и, если у нее нет специальных приспособлений, ни наш слух, ни Пифагор, ни Веркмейстер не в состоянии ничего с ней поделать. И поскольку у фанфары нет ни клапанов, ни вентилей, она до сих пор играет в натуральном строе.
А кроме проблем, остались интересные вопросы. Математически все тональности равны, но почему у многих композиторов есть любимые? Почему тональности, даже если все они минорные, кажутся им разными — от грустных до глубоко трагических? А мажорные — от радостных до страстных и возвышенных?
Но мы не будем пытаться отвечать на эти вопросы. Там, где речь идет о тонкостях и оттенках человеческих чувств, арифметика становится бессильной.
С. ГАЗАРЯН
Рисунок Г. АЛЕКСЕЕВА


